Sorry Terry, Reverse Engineering Ransomware
Creating ransomware in Rust and reverse engineering it.
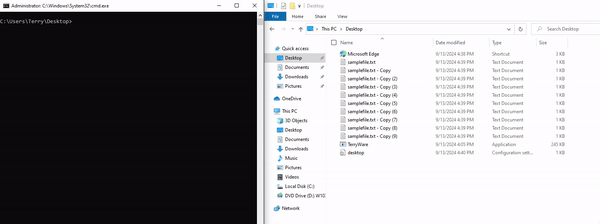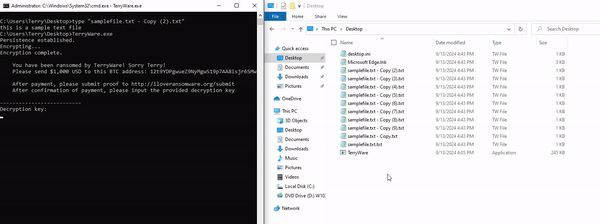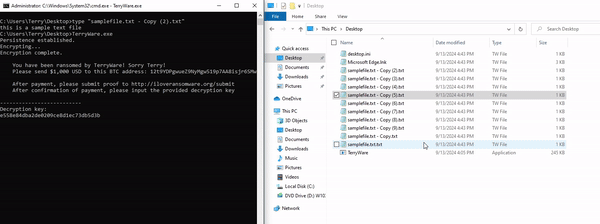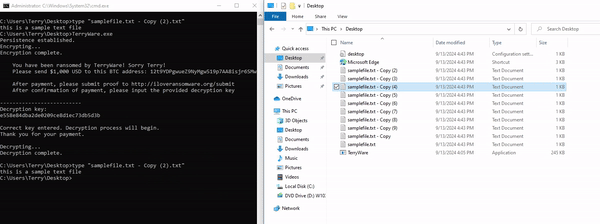
Table of contents
I've spend the past week or so learning Rust, and through some small research I found there weren't a lot of resources/challenges out there for BinEx/RE with Rust. The majority of my experience with BinEx/RE has been centered around analyzing binaries compiled with C on 32-bit architecture. So I took a crack at utilizing my limited Rust knowledge to create some simple ransomware, and primarily used Ghidra to step through the decompiled code.
Ransomware Walkthrough
GitHub Repository
The first step that the program takes, is checking to see if the user "Terry" is present on the system. It conducts this check by checking if the path "C:\Users\Terry\" exists within the C: drive. If this directory isn't present on the target system, the program executes exit(1);, which closes out the program with the error code 1.
If the user "Terry" is present on the system, the program establishes its 'persistence' by loading the current executable into HKCU\Software\Microsoft\Windows\CurrentVersion\Run. This is the registry key in charge of start-up programs, so even if the user reboots their system it will automatically launch at start-up and prompt the user for the decryption key. Additionally, this is also how the program checks to see if it had been previously executed.
If this is a first-time run, it will launch encrypt(), and begin walking through the target directory recursively. If the registry key is already present, it jumps ahead to the message() function to display the ransom note.
Since we're walking through this as if it's a first-time run, we'll step into the encrypt() function. The first line within this function calls another function called generate_aes_key(), which is responsible for creating the AES-128 key that we'll use for both the encryption/decryption functions, as well as the password that Terry will need to enter to get his files back. Realistically, this is terrible design - but it makes things really easy for us.
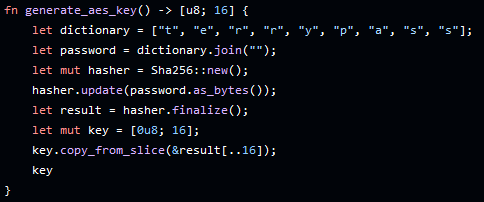
Once we have our AES key of e558e84dba2de0209ce8d1ec73db5d3b (which is the first 16 bytes of the SHA256 hash from "terrypass"), we'll call on encrypt_recursive() to begin the actual process of encrypting his files. This function steps through each file within our target directory of C:\Users\Terry\*, encrypts it with a randomized IV with rand::thread_rng().gen(), and adds the ".TW" file extension for TerryWare. Once this function has run out of files, it calls on the message() function.
This function is pretty simple. It prints out the ransom note, instructing the user to pay $1,000 USD to the listed BTC address, and submit proof to the provided web address. Then, it lists a prompt allowing the user to type in their decryption key that they're given upon payment. The user's input is checked against the AES-128 key, which has been formatted from bytes into a readable hexadecimal string.
After the user enters the correct decryption key, the program then executes decrypt(). This function works nearly the same as our encrypt function, except backwards. It targets each file within C:\Users\Terry and extracts the IV for decryption, replaces the file extension back to its original form, then writes the decrypted data.
Reverse Engineering TerryWare
Now, before I begin I do want to make one quick note. I am not a great reverse engineer, and I don't have too much experience with it. But I've always loved application security & binary exploitation, and I want to demonstrate that it's not as daunting as it appears.
For me, I like to start by finding the strings within a binary, as it can help provide some context:
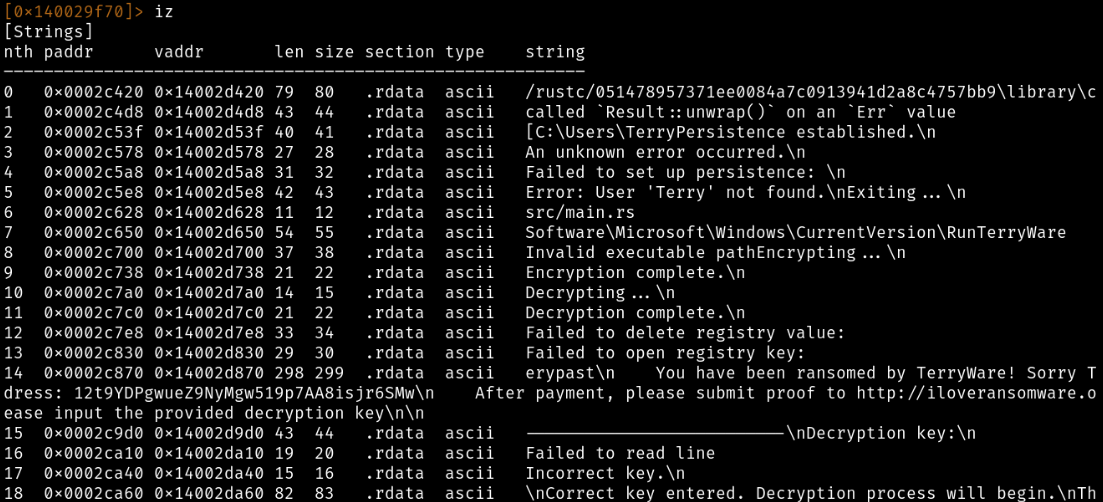
Looks like we already got a decent look at what this program does. We have a couple of virtual addresses of where these strings live, and we can fire up Ghidra and head to those to get the bigger picture on where these are being called. Using Ghidra, we can hit Ctrl+Shift+E and search for strings, I'll look for that BTC address (12t9...6SMw) and see where that gets us:
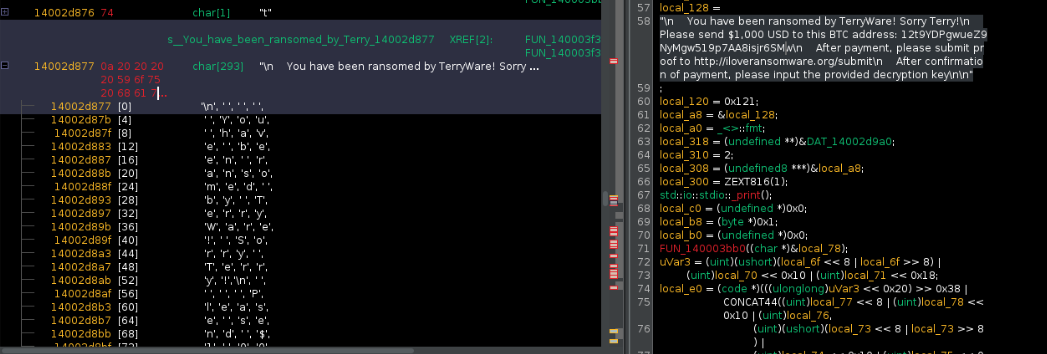
Looks like we found where that string was in the decompiled code. To make your life easier, you can right-click the pane with the decompiled code, which I've renamed has_ransom_note. If we scroll a little bit on that right-hand pane, we found a very promising snippet pointing to an address:
local_318 = &PTR_s__Correct_key_entered._Decryption_14002 dab8;
local_310 = 1;
local_308 = (undefined8 ***)0x8;
local_300 = ZEXT816(0);
std::io::stdio::_print();
FUN_140003bb0((char *)&local_118);
libaes::Cipher::new_128(&local_318,(undefined (*) [16])&local _118);
local_a8 = &PTR_s_Decrypting..._14002d7b0;
Looking back at the dumped strings we got, as well as the original code in the linked repo, this starts to look familiar. Once the user enters the correct decryption key, it calls
println!() to provide output, then breaks the loop. Once that loop is broken, we step directly into decrypt(), which is called on the 6th line within the code snippet. We can double click it and Ghidra will take us to that function.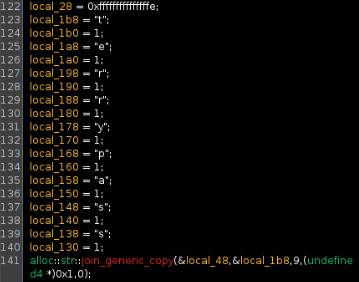
Jumping to the function, we can already see the declaration of the "terrypass" dictionary. The instruction directly below of
alloc::str::join_generic_copy(...); is TerryWare's method for joining the 9-char dictionary into a single string. Moving forward in the code also takes us to this: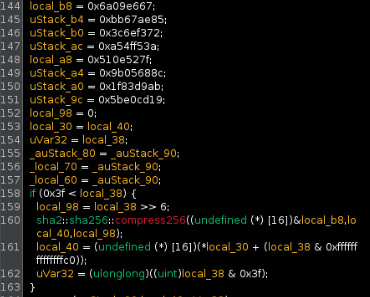
There are two things going on here, for one purpose. The first step is initializing the use of the SHA-2 algorithm, as seen by the declarations of
0x6a09e667, 0xbb67ae85, etc. as well as the if-statement processing the input data. This long block is the result of the following code seen in the repo: let mut hasher = Sha256::new(); hasher.update(password.as_bytes()); let result = hasher.finalize();, meaning we're stepping through the decryption functionality as expected, since we're executing the generate_aes_key() function. Scrolling through, there are additional steps shown in the decompiled code, such as padding, computation, hash finialization, and memory deallocation - but we don't get much further than that. We can rename this function to sha_computation() and move on.Directly after our newly defined function, we come across
libaes::Cipher::new_128(&local_318,(undefined (*) [16])&local _118);. Using context clues, it looks like this is where the AES key is generated for decryption. The code is calling the libaes module for initializing the 128 bit key, and within the parentheses we can see that the pointer local_118 is being used to input the correct key into &local_318. We can update our decompiled code to rename these variables key and key_var respectively.So we've located where our AES key is generated and stored. Let's scroll up a bit and check for the comparison on user input:
if (((HKEY **)
_Size == local_98) && (iVar2 = memcmp(_Dst,local_f0,(size_t)local_98), iVar2 == 0)
) break;
I've highlighted points of interest in this function:
_Size most likely refers to the size of the input key, local_98 appears to be a reference to the key/value, _Dst is where the user input is stored, and local_f0 is most likely the stored key thats being used for comparison.Combining everything together, we have a decent amount to go off of. We started by finding the SHA computation through our renamed function of
sha_computation((char *)&local_78);, which performs the hashing of input to produce its value, which is then used to derive the AES key. Following the computation, the code initializes the AES cipher with libaes::Cipher::new_128(&local_318, (undefined (*) [16])&local_118);. Here, local_118 is used to store the generatred AES key, derived from the SHA-2 computation. While the exact mechanism for deriving a 128-bit key from the 256-bit hash is not fully detailed, it often involves truncation or selection of a portion of the hash. The local_318 pointer represents the AES cipher initialized with the key. Then we went forward and found our comparison between the key and user input: if (((HKEY **)_Size == local_98) && (iVar2 = memcmp(_Dst, local_f0, (size_t)local_98), iVar2 == 0)) break;.Thus, the AES key used in actual decryption appears to also be used as the key for user input. While we can't see the final output of "terrypass" in SHA256 within the decompiled code, we can use an online tool to convert the string, and trim the first 16 bytes into: e558e84dba2de0209ce8d1ec73db5d3b.
Thank you for reading, if you have any questions/comments/concerns on this post - please reach out to me via LinkedIn.
-connor